MMDにおいて、モデルの見た目に大きく関わる「スフィアマップ」について解説します。
スフィアマップとは何か
PMXエディタでは、ここでスフィアマップを設定できます。
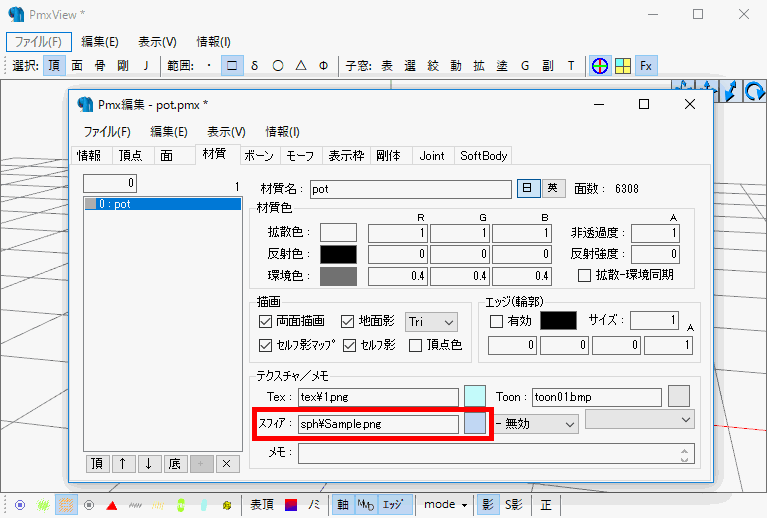
スフィアとは英語で「球」をあらわします。
配布されているスフィアマップを見てみると、どれも球面に何かを映したように見えるはずです 。
スフィアマップを使うと、低負荷で手軽に映り込みを表現できます。
スフィアマップの仕組み
簡単にですが、スフィアマップの仕組みを説明いたしましょう。
スフィアマップは簡単に言うと、鏡のような見た目を「疑似的に」再現する方法です。
どこが「疑似的に」なのかというと、映り込む景色です。
反射したものを表現するというのは非常に高度で複雑な処理を伴います。
それをあらかじめ「この景色を移しこむ」と画像としてセットすることで簡単に映り込みを表現させることができます。
ここで手鏡を思い出してください。
手鏡を傾けると、映っている景色が変わりますよね?
また、鏡を固定して鏡を見る方向を変えても映り込む景色は変わります。
映っている景色は、目線と鏡の面の角度によって決まるのが分かると思います。
MMDでモデルを見た場合、そのモデルの表面のポリゴンはカメラに対して角度があります。
その角度によって、スフィアマップ画像のどのピクセルを表示するかが決まるわけです。
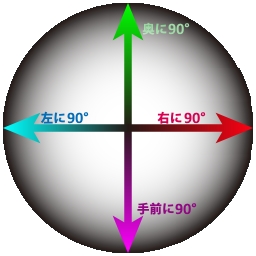
「ポリゴンがカメラに対してどれだけ傾いているかによって、リアルタイムに反映されるテクスチャ」
というのがスフィアマップなのです。
加算スフィアと乗算スフィア
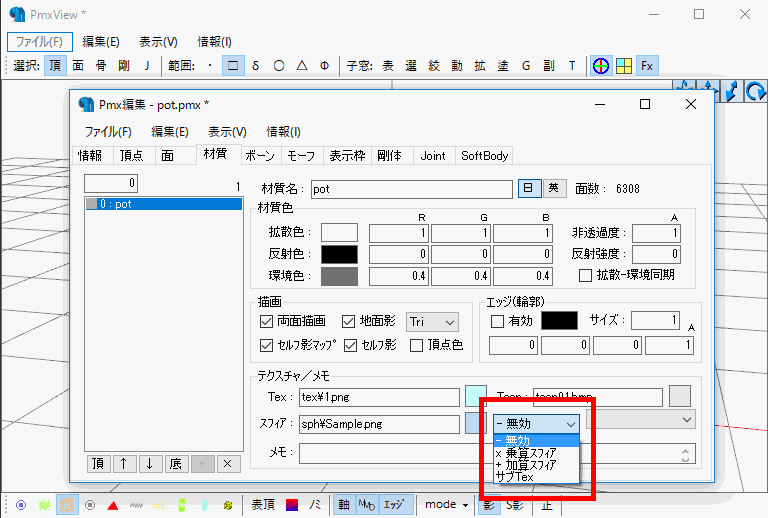
PMXエディタのこの部分から、「加算」と「乗算」を選ぶことができます。 この2つの違いについて解説します。
「加算」と「乗算」
「加算」とは足し算。「乗算」とは掛け算のことですが、画像処理関連では画像の重ね方を意味します。
普通に2枚の画像を重ねると、上に重ねた画像で下にある画像が隠れてしまいます。
しかし上に重ねる画像を「加算」や「乗算」に設定すると、下の画像を完全に隠すことなく重ねることができます。
| 画像1 | 画像2 | 加算 | 乗算 |
|---|---|---|---|
 |  |  |  |
画像をはピクセルというドットの集まりで、そのドットはRGB(赤と緑と青)の色情報を持っています。
画像を重ねたときに、下にあるピクセルを(R1,G1,B1)、上にあるピクセルを(R2,B2,G2)とすると
加算の場合、( R, G, B) = ( R1, G1, B1) + ( R2, B2, G2)
乗算の場合、( R, G, B) = ( R1*R2, G1*G2, B1*B2) / 255
となります。 因みにRGBの成分が255を超えると255になります。
加算スフィアと乗算スフィアの使い分け
加算スフィアは「光の映り込み」。
乗算スフィアは「景色の映り込み」
というのが直感的に分かりやすい表現です。
金属の球体に景色が映り込んでいるだったりと、何か球状の物体に見える場合は大抵「乗算スフィア」です。
全体的に黒く、白い点や線が描かれているスフィア画像は、大抵「加算スフィア」となります。
次のようなポットのモデルを用意しました。

これに以下のスフィアを適用してみます。
左から、「金属」「ガラス」「漆」のスフィアマップです。
金属と漆のスフィアマップは、それ自体が材質の質感を表しています。
そのため、乗算スフィアにするのが正解です。加算にしてしまうと白っぽくなってしまいます。
ガラスのスフィアマップは、質感を表しているのではなく、光の反射を表した画像です。
ですので、加算マップとして適用するのが正解です。
乗算マップにしてしまうと、真っ黒な物体になってしまいます。
しかし、「つやつやした黒い質感」を表したいのであれば乗算が正解となります。
スフィアマップの弱点
スフィアマップは非常に手軽ですが、正確ではないという弱点があります。
映っている景色、もしくは反射している光が、実際の光源や景色とは違うというのはもちろんですが、
一番の弱点はカメラを回転させると違和感があるということです。
例えば、鏡のように磨かれた金属球を思い浮かべてみてください。
その金属球の周りをぐるっと1周すると、映り込む景色が変わっていくと思います。
しかし、スフィアマッピングではそのようなことは起こりません。
常に映し出される景色は固定になります。
これが一番違和感を覚えやすいのは、モデルやカメラのZ軸回転です。(顔を傾けたときの回転)
現実には、上のほうに空。下のほうに地面が金属球には映し出されます。
逆立ちしてみると、下に空があり、上に地面があるわけですから、 当然金属球には下のほうに空。上のほうに地面が映し出されるはずです。
しかしスフィアマップではそうはなりません。
視界の下に空、上に地面があるのに、金属球に移った景色はそのままです。
正確に鏡面反射を行いたい場合には、MMEの力を借りる必要があります。
| 正確な鏡面反射 | スフィアマップでの表現 |
|---|---|
 |
 |
まとめ
- スフィアマップはカメラとポリゴンの角度によって動的に表示される。
- 単純な映り込みは乗算スフィア。強い光の反射は加算スフィアを使う。
- 正確な反射表現はMMEが必須。








